Groo
리스트에 대해서 본문

안녕하세요, 오늘은 정말 오랜만에 새로운 자료구조에 대해서 알아보려고 합니다.
그것은 바로 리스트 자료구조이며 프로그래밍에서 정말 중요한 개념 중 하나입니다.
📊 리스트란?
간단히 설명하면 리스트는 데이터를 순서대로 나열한 자료구조입니다. 여러분들이 프로그래밍을 할 때 자주 사용하는 배열을 예로 들 수 있습니다. 같은 자료형을 가진 여러 개의 값을 저장하기 위해 변수를 일일이 생성하지 않고 배열이라는 곳에 데이터를 순서대로 저장할 수 있는 것처럼 말이죠. 또한 Java에서 자주 사용하는 ArrayList 또한 리스트 자료구조의 개념을 바탕으로 만들어졌습니다.
int[] arr = new int[7];
ArrayList<Integer> arrayList = new ArrayList<>();이처럼 리스트는 프로그래밍을 할 때 이미 우리가 자주 사용하고 있으며 친근한 존재와 같습니다. 하지만 다수의 사람들이 기초적인 리스트에 대해서만 알고 있을 뿐 심화적인 내용에 대해서는 잘 알지 못합니다. 그렇기에 지금부터 천천히 알아보도록 합시다.
⛳️ 선형 리스트란?
가장 먼저 알아볼 리스트는 선형 리스트입니다. 선형 리스트는 리스트 자료구조에서의 가장 기초적인 개념이라고 할 수 있습니다. 바로 위에서 예시로 설명했던 배열과 Java에서의 ArrayList를 대표적인 선형 리스트라고 합니다. 선형 리스트 내부의 각각의 데이터는 서로 간의 연결 관계가 존재하지 않으며 순수한 리스트의 개념처럼 리스트 내부에 데이터를 일정하게 나열해둔 구조일 뿐입니다.

선형 리스트는 위의 사진 속 구조처럼 데이터들이 처음부터 마지막까지 일정한 순서로 나열되어 있습니다. 이제 어느 정도 선형 리스트에 대해서 이해가 되셨나요? 그럼 이번에는 배열로 간단하게 선형 리스트를 구현해 각종 기능들을 구상해보도록 하겠습니다.
class Student {
int age;
String name;
Boolean gender;
public Student(int age, String name, Boolean gender) {
this.age = age;
this.name = name;
this.gender = gender;
}
}
public class StudentTester {
public static void main(String[] args) {
Student[] studentList = {
new Student(19, "김주엽", false),
new Student(19, "김성헌", false),
new Student(19, "최진우", false),
new Student(18, "신중빈", false),
new Student(18, "박상아", true),
new Student(19, "이영은", false),
new Student(19, "김혜선", true)
};
}
}StudentTester 클래스의 main 함수를 보면 자료형이 Student 클래스이고 요소의 개수가 7인 studentList 배열이 존재합니다. 이 상황에서 만약 배열 속 인덱스 값이 2인 최진우 학생이 전학을 간다고 하면 기존의 배열은 어떻게 될까요? 최진우 학생 바로 뒤에 위치한 배열 속 인덱스 값이 3인 신중빈 학생이 한 칸 앞으로 올 것이며 뒤에 있는 학생들 마찬가지로 자리를 한 칸씩 앞으로 당깁니다.

최진우 학생이 전학을 갔으므로 기존의 배열 크기가 7이던 studentList의 6번째 인덱스 자리는 공백이 됩니다. 며칠 뒤 새로운 학생이 공백을 막기 위해 전학을 왔으나 그 학생은 정말 독특하게도 0번째 인덱스 자리에 위치하고 싶어 합니다. 기존의 학생들은 자리 이동이 정말 귀찮았지만 전학생의 부탁을 들어주기 위해 0번째 자리에 위치한 김주엽 학생을 시작으로 한 칸씩 모두 뒤로 물러납니다.

이처럼 리스트의 가장 기초적인 선형 리스트는 특정 요소를 리스트에서 삭제하거나 새롭게 삽입하는 경우 많은 양의 요소들을 뒤로 밀거나 앞으로 당겨야 하는 불필요한 작업이 생기므로 과정이 복잡하기도 하면서 효율적이지 못하다고 많이 평가되고 있습니다.
선형 리스트의 단점
1) 리스트에 삽입될 수 있는 최대 요소 개수를 미리 알아야 합니다.
2) 요소의 삽입, 삭제에 따라 많은 요소를 옮겨야 하기 때문에 효율이 좋지 않습니다.
🧲 연결 리스트란?
이번에는 리스트 자료구조의 심화 내용인 연결 리스트에 대해서 알아보겠습니다. 연결 리스트는 앞에서 배웠던 선형 리스트처럼 데이터가 일정하게 나열되어 있는 원초적인 리스트의 개념은 당연히 포함하고 있으며 추가적으로 선형 리스트가 가지고 있지 않은 차별화된 한 가지의 특징을 지니고 있습니다. 그 한 가지가 바로 리스트 속 데이터 간의 연결 개념입니다. 어렵지 않으니 천천히 알아보시죠!
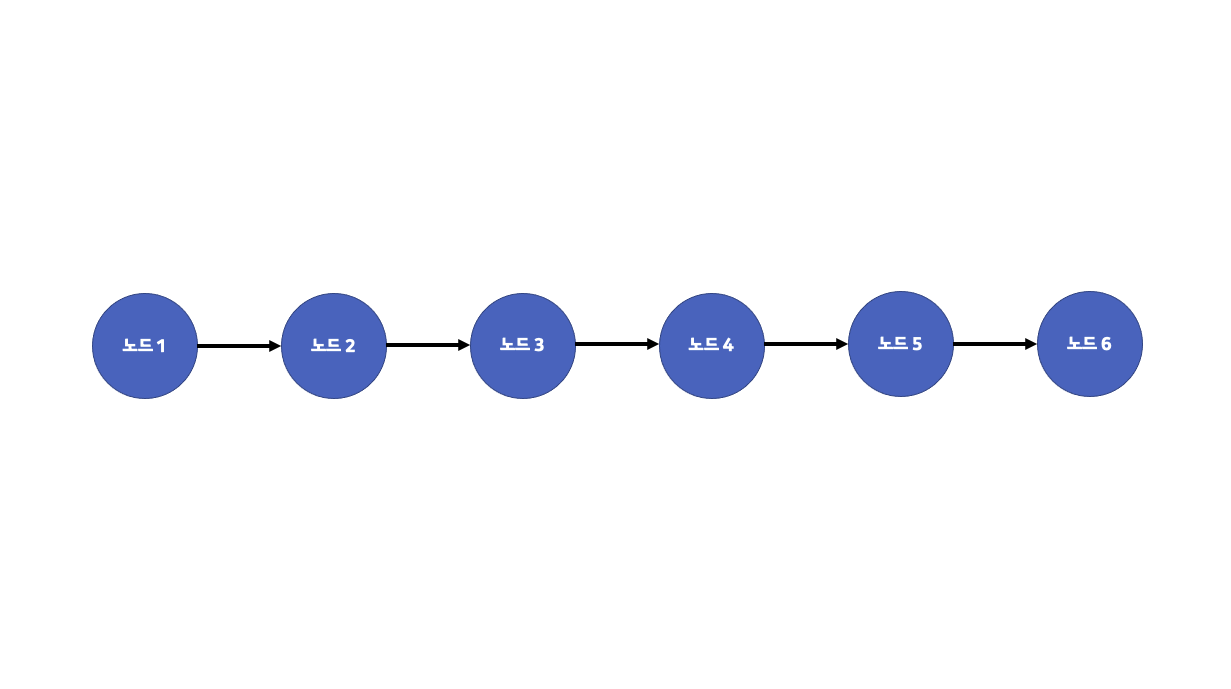
연결 리스트는 기존의 선형 리스트와는 달리 리스트 속 데이터들이 한 방향으로 연결되어 있는 모습을 볼 수 있습니다. 또한 연결 리스트 내부의 각각의 데이터를 노드라고 부릅니다. 즉 리스트 내부의 각각의 노드들이 한 방향으로 연결되어 있는 것을 연결 리스트라고 정의할 수 있습니다. 노드의 종류에 따라 포인터 연결 리스트 또는 커서 연결 리스트 등 다양한 연결 리스트를 만들 수 있습니다.
# 포인터 연결 리스트
포인터 연결 리스트는 아래와 같은 Node 클래스를 가지고 있습니다. Node 클래스 옆의 E는 제네릭을 뜻하며 클래스 내부의 멤버 변수 data의 자료형인 것을 볼 수 있습니다. data 변수는 한 노드의 고유 값을 의미하는 반면에 실질적인 value가 아닌 외부 데이터에 대한 reference 형태입니다. 또한 next 변수는 리스트 상에서 자신의 뒤에 위치한 자기 자신과 같은 클래스형의 인스턴스 노드를 참조하는 역할을 하며 next 변수도 마찬가지로 reference 형태입니다. 즉 data와 next는 모두 참조형 변수라고 할 수 있습니다.
class Node<E> {
E data;
Node<E> next;
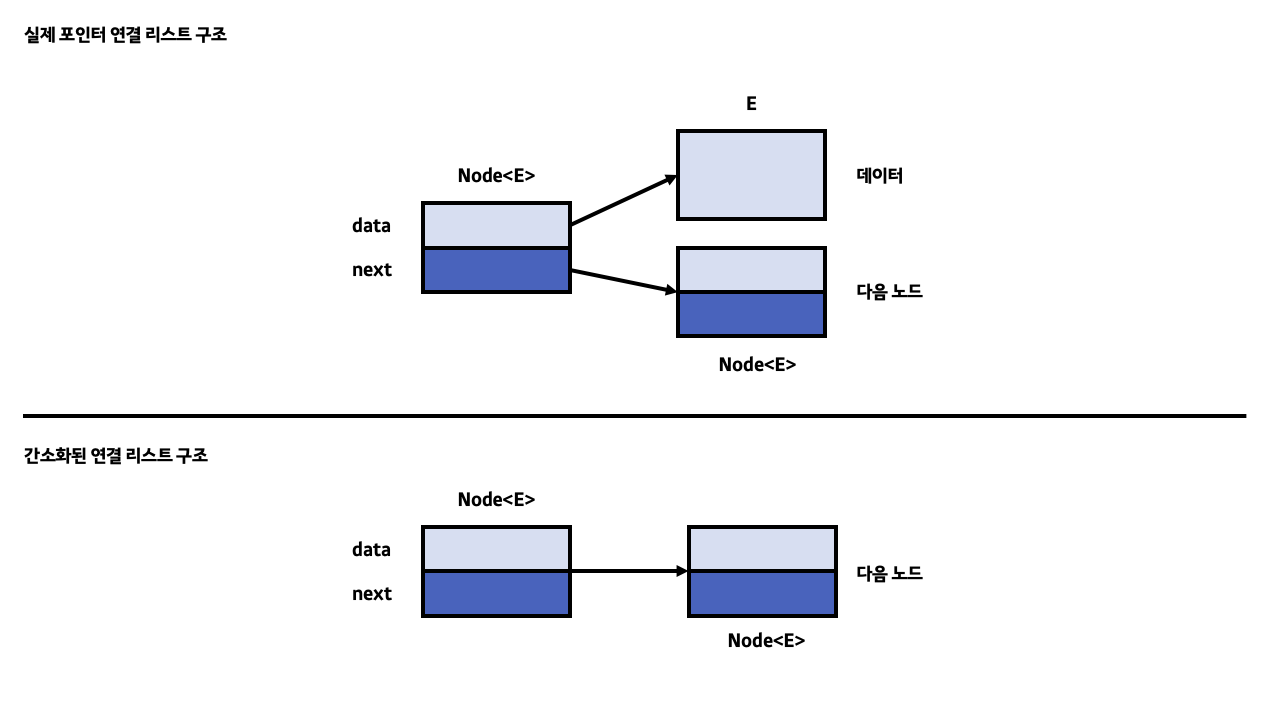
}아래는 실제 포인터 연결 리스트에서 한 노드가 다음 노드를 가리키는 구조를 표현한 것입니다. 정확한 구조는 아래의 사진에서 위의 구조가 맞지만 그림으로 포인터 연결 리스트의 구조를 표현할 때 복잡해 보이는 단점이 있어 보통 간소화된 구조를 많이 사용합니다.
또한 포인터 연결 리스트뿐만 아니라 모든 연결 리스트에서 가장 앞에 위치한 노드를 머리 노드라고 하며 가장 뒤에 위치한 노드를 꼬리 노드라고 부릅니다. 꼬리 노드의 next 값으로 NULL을 대입해 더 이상 노드가 없으며 자신이 마지막이라는 것을 입증합니다.
아래의 코드는 지금까지 공부한 포인터 연결 리스트의 개념을 바탕으로 각종 기능들을 구현해본 것입니다. 메서드 별로 설명을 하면 좋으나 양이 많기도 하고 위에서 얘기했던 개념만으로도 충분이 이해할 수 있을 것이라고 생각해 상세한 설명은 건너뛰겠습니다. 그러나 어떤 역할을 하는 메서드인지에 대해 주석으로 간략히 남겨두었기에 천천히 코드를 분석하며 해석해보시기 바랍니다.
그래도 한 가지 설명하자면 LinkedList<E> 클래스의 멤버 변수인 head는 포인터 연결 리스트에서 머리 노드에 위치한 노드를 가리키는 역할을 합니다. 또한 crnt 변수 역시 현재 포인터 연결 리스트에서 포커스를 받고 있는 특정 노드를 가리키는 역할을 합니다. 이 둘은 아래의 메서드들에서 자주 참조될 것이니 아주 중요하며 현재는 리스트에 노드가 아무것도 없기에 NULL로 초기화해줍니다.
// 포인터 연결 리스트 클래스
public class LinkedList<E> {
// 노드 클래스
class Node<E> {
private E data;
private Node<E> next;
Node(E data, Node<E> next) {
this.data = data;
this.next = next;
}
}
// 머리 노드 & 선택 노드
private Node<E> head;
private Node<E> crnt;
// 생성자
public LinkedList() {
head = crnt = null;
}
// 검색을 수행하는 메서드
public E search(E obj, Comparator<? super E> c) {
Node<E> ptr = head;
while (ptr != null) {
if (c.compare(obj, ptr.data) == 0) {
crnt = ptr;
return ptr.data;
}
ptr = ptr.next;
}
return null;
}
// 머리에 노드를 삽입하는 메서드
public void addFirst(E obj) {
Node<E> ptr = head;
head = crnt = new Node<>(obj, ptr);
}
// 꼬리에 노드를 삽입하는 메서드
public void addLast(E obj) {
if (head == null) {
addFirst(obj);
} else {
Node<E> ptr = head;
while (ptr.next != null) {
ptr = ptr.next;
}
ptr.next = crnt = new Node<>(obj, null);
}
}
// 머리 노드를 삭제하는 메서드
public void removeFirst() {
if (head != null) {
head = crnt = head.next;
}
}
// 꼬리 노드를 삭제하는 메서드
public void removeLast() {
if (head != null) {
if (head.next == null) {
removeFirst();
} else {
Node<E> ptr = head;
Node<E> pre = head;
while (ptr.next != null) {
pre = ptr;
ptr = ptr.next;
}
pre.next = null;
crnt = pre;
}
}
}
// 특정 노드를 삭제하는 메서드
public void remove(Node<E> p) {
if (head != null) {
if (head == p) {
removeFirst();
} else {
Node<E> ptr = head;
while (ptr.next != p) {
ptr = ptr.next;
if (ptr == null) return;
}
ptr.next = p.next;
crnt = ptr;
}
}
}
// 선택 노드를 삭제하는 메서드
public void removeCurrentNode() {
remove(crnt);
}
// 모든 노드를 삭제하는 메서드
public void clear() {
while (head != null) {
remove(crnt);
}
crnt = null;
}
// 선택 노드를 하나 뒤쪽으로 이동하는 메서드
public boolean next() {
if (crnt == null || crnt.next == null) {
return false;
}
crnt = crnt.next;
return true;
}
// 선택 노드를 표시하는 메서드
public void printCurrentNode() {
if (crnt == null) {
System.out.println("선택한 노드가 없습니다.");
}
else {
System.out.println(crnt.data);
}
}
// 모든 노드를 표시하는 메서드
public void dump() {
Node<E> ptr = head;
while (ptr != null) {
System.out.println(ptr.data);
ptr = ptr.next;
}
}
}# 커서 연결 리스트
앞에서 연결 리스트는 노드의 종류에 따라 다양해질 수 있다고 말했습니다. 이번에는 각 노드를 배열 안의 요소에 저장하고 그 요소를 이용하여 각종 기능들을 수행하는 커서 연결 리스트에 대해서 알아보겠습니다. 아래는 커서 연결 리스트의 노드 클래스입니다. 바로 위에서 살펴보았던 포인터 연결 리스트와는 사뭇 달라서 당황스러울 수도 있습니다. 한 개씩 천천히 살펴볼 테니 걱정하지 마세요!
커서 연결 리스트의 Node 클래스 또한 제네릭 형태로 data 변수의 자료형인 것을 볼 수 있습니다. data 변수는 이전과 마찬가지로 실질적인 value가 아닌 외부 데이터에 대한 reference입니다. 그리고 next 변수는 커서 연결 리스트에서 가장 중요한 커서 역할을 맡고 있으며 독특하게도 자료형이 int형인 것을 볼 수 있습니다. 그 이유는 커서 연결 리스트에서의 각 노드들은 한 배열 안에 모두 저장되어 있기에 자신의 뒤에 위치한 특정 노드를 가리키기 위해서는 배열 속 해당 노드의 인덱스 값만 알고 있으면 되기 때문입니다.
여기서 헷갈리실 텐데 커서 연결 리스트의 각각의 노드들이 구성하는 연결 형태가 배열 속 노드들이 저장되어 있는 순서와는 관계가 없다는 것을 기억해주시기 바랍니다. 단지 특정 노드를 지칭할 때 배열 속에 해당 노드가 위치한 인덱스 값을 활용하는 것뿐입니다. 또한 커서 연결 리스트에서 꼬리 노드의 next 값은 배열 인덱스로 존재할 수 없는 -1로 지정하여 마지막 노드라는 것을 입증합니다.
class Node<E> {
E data;
int next;
int dnext;
}Node 클래스의 마지막 멤버 변수인 dnext 변수는 커서 연결 리스트에서 새롭게 추가되었습니다. 그 이유는 커서 연결 리스트는 포인터 연결 리스트와는 달리 두 개의 연결 리스트가 내부에서 함께 동작하기 때문입니다. 첫 번째 연결 리스트는 현재 배열 속에 존재하는 노드를 통해 연결을 이루는 일반적인 형태인 반면에 두 번째 연결 리스트는 기존의 배열에서 삭제된 노드들의 자리를 재활용하기 위해 연결을 이루는 독특한 형태입니다. 보통 전자의 리스트가 메인이며 후자의 리스트는 전자의 리스트를 서포트 역할을 해줍니다.
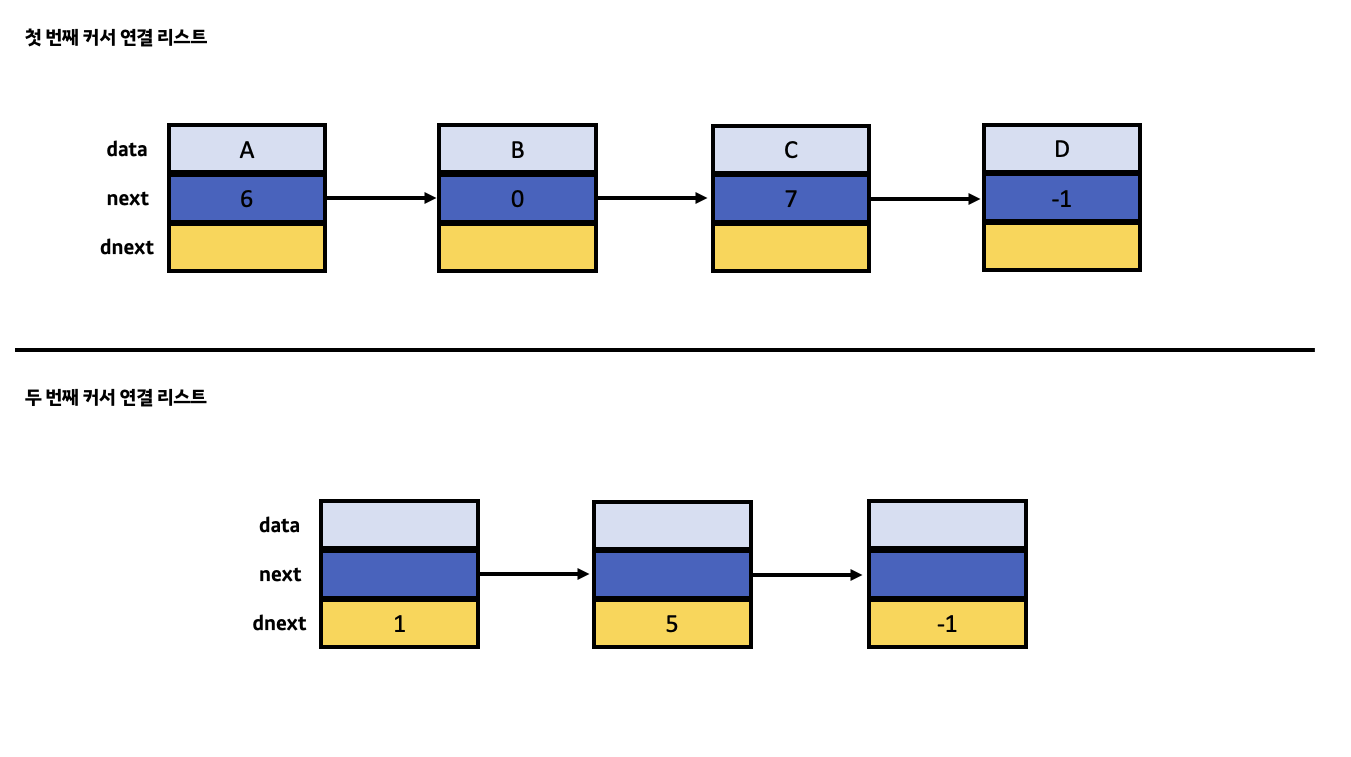
전자의 리스트에서 배열 속 존재하는 노드를 연결하기 위해 next 커서를 사용한 것처럼 후자의 리스트에서는 기존의 배열에서 삭제된 노드들을 연결하기 위해 dnext 커서를 사용합니다. dnext 커서는 next 커서처럼 int 자료형을 가지고 있으며 자신의 뒤에 위치한 특정 노드의 기존 배열 속 인덱스 값을 가리킵니다. 이때 만약 해당 노드가 후자의 리스트에서 꼬리 노드라면 -1로 지정합니다.
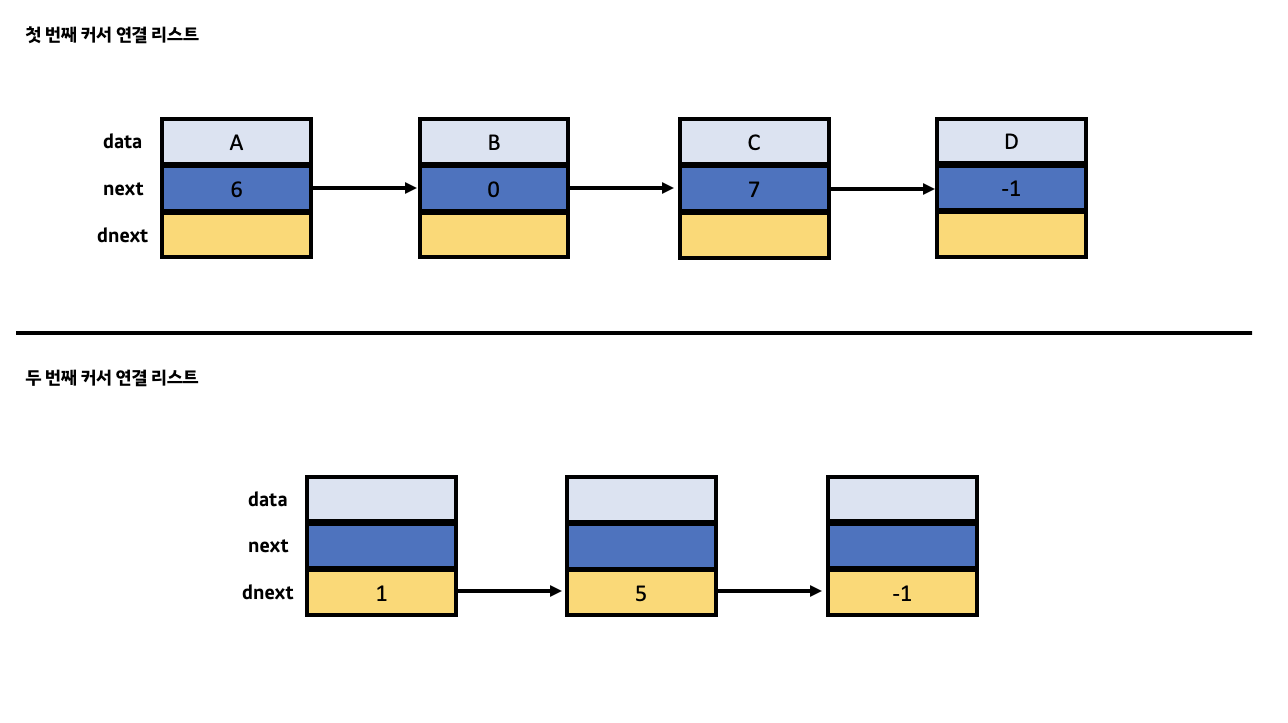
많이 햇갈리실 것 같아 전체적인 흐름을 정리하면 전자의 리스트에서 특정 노드가 삭제된다면 해당 노드의 메모리 전체가 기존의 배열에서 삭제되는 것이 아닌 data, next 변수의 값이 NULL로 변경되며 해당 노드는 후자의 리스트에 추가되게 됩니다. 이러한 과정에서 dnext 커서는 후자의 리스트에서 자신의 뒤에 위치하는 노드를 가리키게 됩니다. 그 후 만약에 전자의 리스트에서 새로운 노드를 추가할 때 매번 배열의 크기를 늘려 노드를 추가하는 것이 아닌 후자의 리스트 속 기존의 삭제된 노드의 배열 자리를 재활용합니다.
아래의 코드는 지금까지 배운 커서 연결 리스트의 개념을 바탕으로 각종 기능들을 구현해본 것입니다. 이번에도 역시 상세한 설명은 따로 하지 않을 것이며 간략히 남겨둔 주석과 함께 코드를 천천히 읽어보면서 커서 연결 리스트의 구조를 되새겨보기 바랍니다.
// 커서 연결 리스트 클래스
public class AryLinkedList<E> {
// 노드 클래스
class Node<E> {
private E data;
private int next;
private int dnext;
void set(E data, int next) {
this.data = data;
this.next = next;
}
}
private Node<E>[] n; // 리스트의 본체
private int size; // 리스트의 용량
private int max; // 사용 중인 꼬리 레코드
private int head; // 첫 번재 리스트의 머리 노드
private int crnt; // 첫 번째 리스트의 선택 노드
private int deleted; // 두 번째 리스트의 머리 노드
private static final int NULL = -1; // 다음 노드가 없음 & 리스트가 가득 참
// 생성자
public AryLinkedList(int capacity) {
head = crnt = max = deleted = NULL;
try {
n = new Node[capacity];
for (int i = 0; i < capacity; i++)
n[i] = new Node<E>();
size = capacity;
}
catch (OutOfMemoryError e) {
size = 0;
}
}
// 다음에 삽입하는 레코드의 인덱스를 구하는 메서드
private int getInsertIndex() {
if (deleted == NULL) {
if (max < size)
return ++max;
else
return NULL;
} else {
int rec = deleted;
deleted = n[rec].dnext;
return rec;
}
}
// 레코드의 인덱스를 두 번째 리스트에 등록하는 메서드
private void deleteIndex(int idx) {
if (deleted == NULL) {
deleted = idx;
n[idx].dnext = NULL;
} else {
int rec = deleted;
deleted = idx;
n[idx].dnext = rec;
}
}
// 노드를 검색하는 메서드
public E search(E obj, Comparator<? super E> c) {
int ptr = head;
while (ptr != NULL) {
if (c.compare(obj, n[ptr].data) == 0) {
crnt = ptr;
return n[ptr].data;
}
ptr = n[ptr].next;
}
return null;
}
// 머리에 노드를 삽입하는 메서드
public void addFirst(E obj) {
int ptr = head;
int rec = getInsertIndex();
if (rec != NULL) {
head = crnt = rec;
n[head].set(obj, ptr);
}
}
// 꼬리에 노드를 삽입하는 메서드
public void addLast(E obj) {
if (head == NULL)
addFirst(obj);
else {
int ptr = head;
while (n[ptr].next != NULL)
ptr = n[ptr].next;
int rec = getInsertIndex();
if (rec != NULL) {
n[ptr].next = crnt = rec;
n[rec].set(obj, NULL);
}
}
}
// 머리 노드를 삭제하는 메서드
public void removeFirst() {
if (head != NULL) {
int ptr = n[head].next;
deleteIndex(head);
head = crnt = ptr;
}
}
// 꼬리 노드를 삭제하는 메서드
public void removeLast() {
if (head != NULL) {
if (n[head].next == NULL)
removeFirst();
else {
int ptr = head;
int pre = head;
while (n[ptr].next != NULL) {
pre = ptr;
ptr = n[ptr].next;
}
n[pre].next = NULL;
deleteIndex(ptr);
crnt = pre;
}
}
}
// 특정 노드를 삭제하는 메서드
public void remove(int p) {
if (head != NULL) {
if (p == head)
removeFirst();
else {
int ptr = head;
while (n[ptr].next != p) {
ptr = n[ptr].next;
if (ptr == NULL) return;
}
n[ptr].next = NULL;
deleteIndex(p);
n[ptr].next = n[p].next;
crnt = ptr;
}
}
}
// 선택 노드를 삭제하는 메서드
public void removeCurrentNode() {
remove(crnt);
}
// 모든 노드를 삭제하는 메서드
public void clear() {
while (head != NULL)
removeFirst();
crnt = NULL;
}
// 선택 노드를 하나 뒤쪽으로 이동하는 메서드
public boolean next() {
if (crnt == NULL || n[crnt].next == NULL)
return false;
crnt = n[crnt].next;
return true;
}
// 선택 노드를 출력하는 메서드
public void printCurrentNode() {
if (crnt == NULL)
System.out.println("선택 노드가 없습니다.");
else
System.out.println(n[crnt].data);
}
// 첫 번째 리스트의 모든 노드를 출력하는 메서드
public void dump() {
int ptr = head;
while (ptr != NULL) {
System.out.println(n[ptr].data);
ptr = n[ptr].next;
}
}
}# 원형 이중 연결 리스트란?
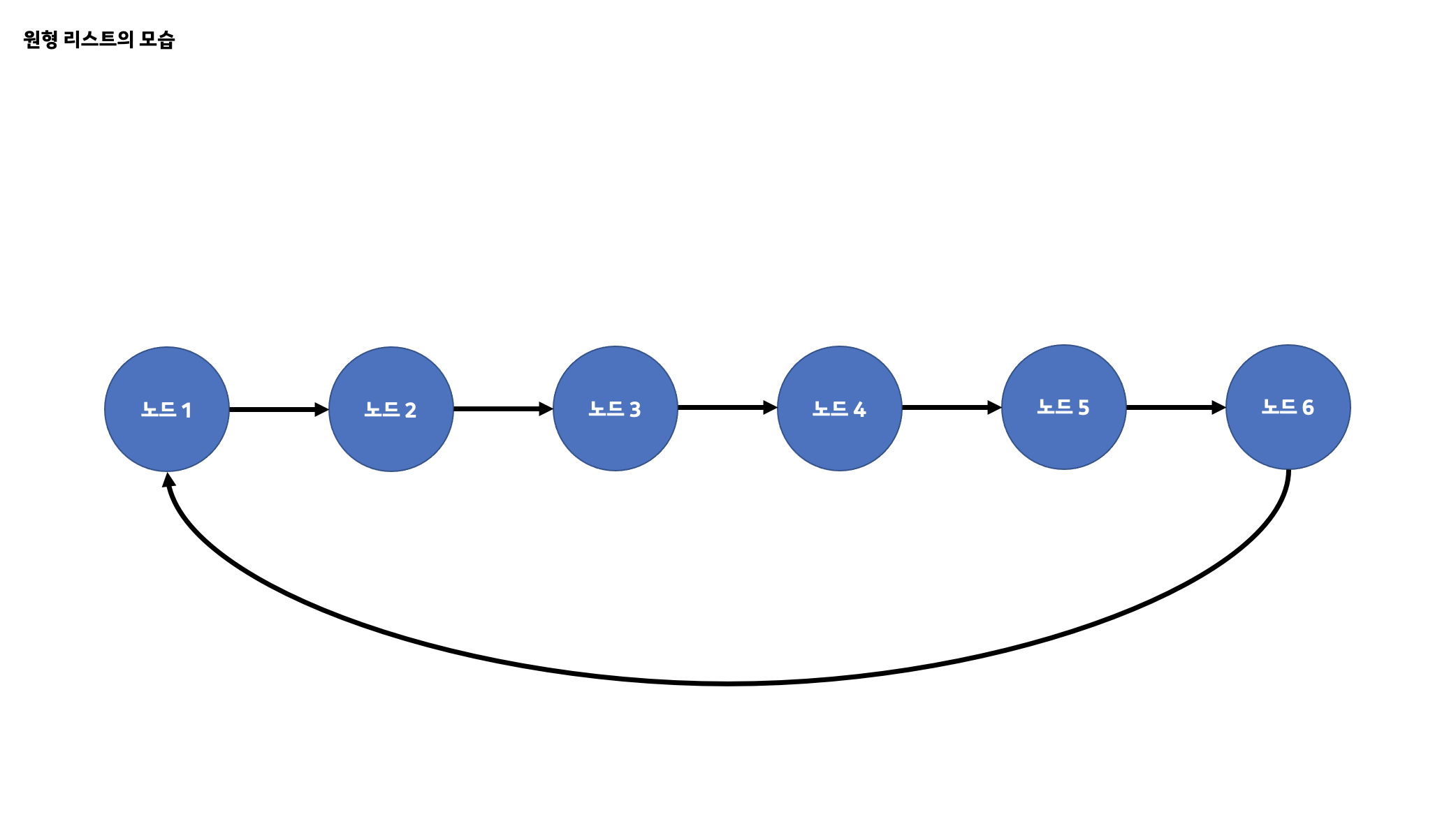
원형 리스트와 이중 연결 리스트가 합쳐진 것을 원형 이중 연결 리스트라고 합니다. 원형 리스트는 연결 리스트에 포함되며 한 가지의 큰 특징을 가지고 있습니다. 그것은 바로 연결 리스트의 꼬리 노드가 머리 노드를 가리키는 것입니다. 기존에 연결 리스트에서는 꼬리 노드 뒤에 더 이상의 노드가 없어 NULL 또는 -1을 가리켰으나 원형 리스트는 리스트의 가장 앞에 위치한 머리 노드를 가리킵니다.
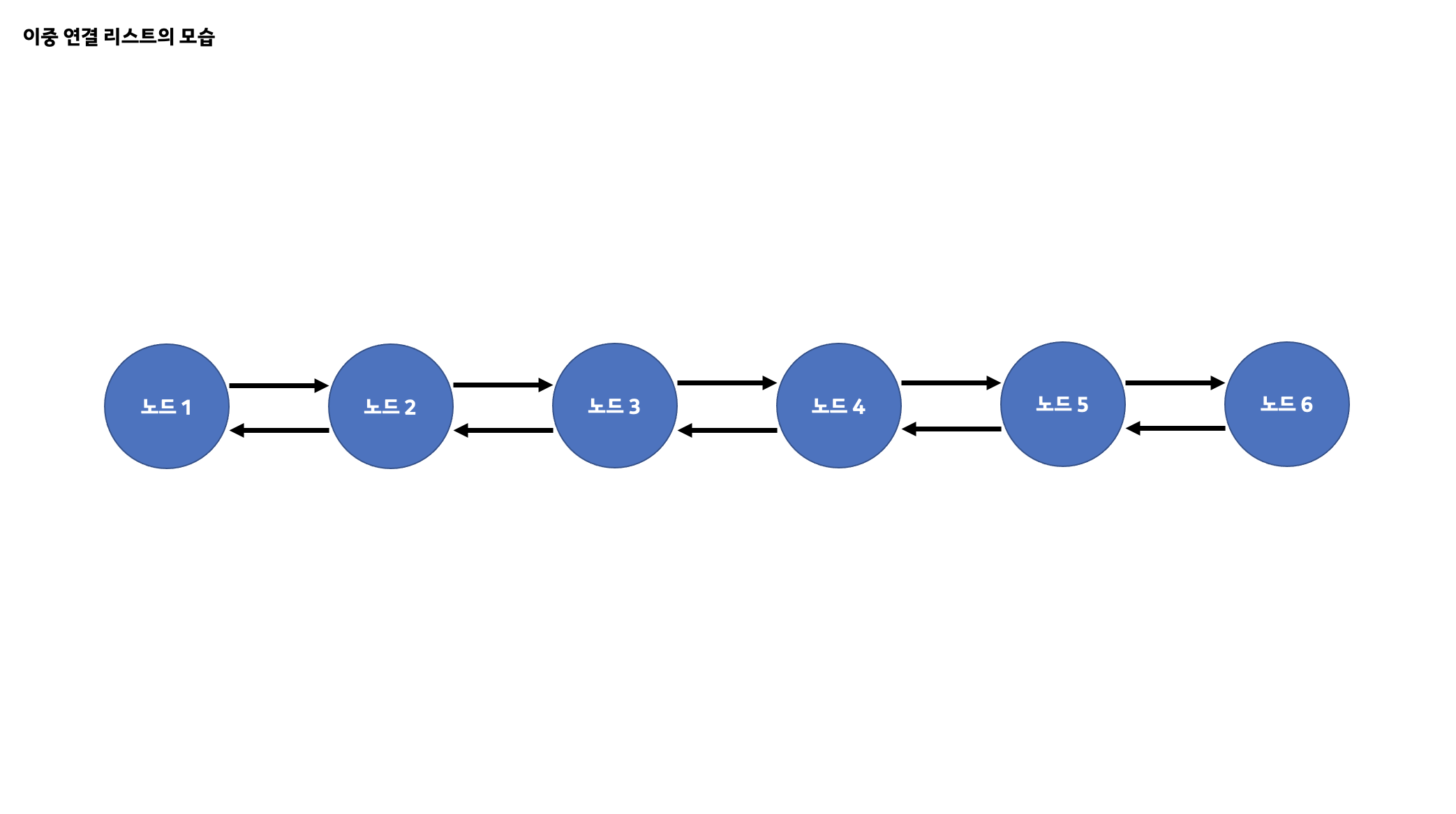
또한 이중 연결 리스트는 기존의 연결 리스트의 단점이었던 리스트 내부에서 특정 노드에 대한 뒤의 노드는 찾을 수 있었지만 앞의 노드는 찾을 수 없다는 한계점을 개선하여 각 노드가 자신의 기준으로 앞 뒤로 위치한 노드를 서로 가리킬 수 있도록 구현되었습니다.
이처럼 기존의 연결 리스트에는 없었던 각각의 핵심 기능을 제공하는 원형 리스트와 이중 연결 리스트가 합쳐진 것이 바로 원형 이중 연결 리스트입니다. 원형 이중 연결 리스트는 위에서 살펴본 내용이 핵심이기에 이를 구현할 수 있는 노드 클래스가 필요합니다.
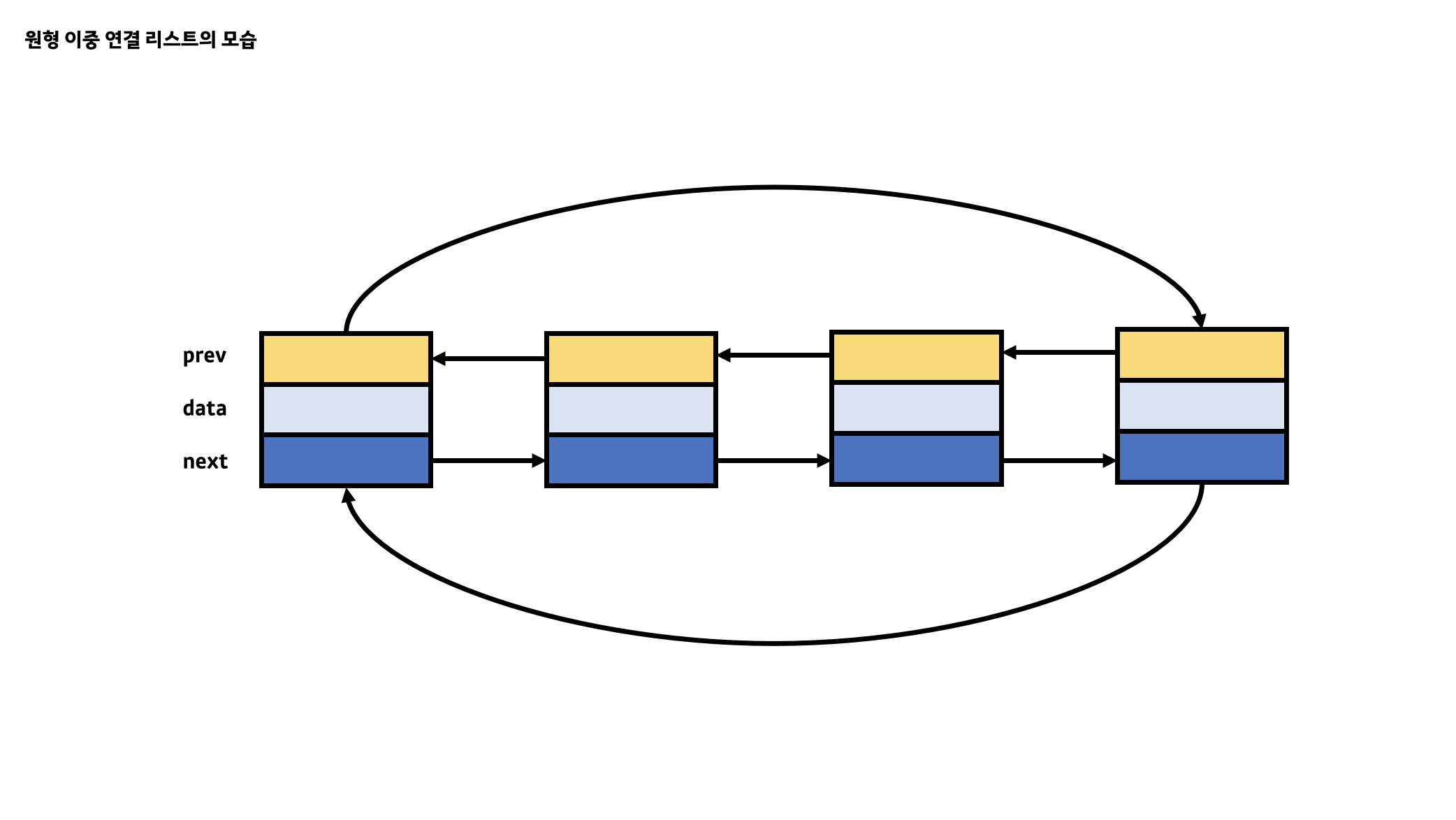
아래는 원형 이중 연결 리스트의 노드 클래스이며 이전에 살펴보았던 포인터 연결 리스트의 노드와 거의 유사합니다. 하지만 prev라는 새로운 변수가 생겼으며 이는 원형 이중 연결 리스트에서 각각의 노드들이 자신의 기준으로 앞에 위치한 노드를 가리킬 수 있도록 돕습니다. 또한 노드 클래스의 data, prev, next 변수는 모두 value 형태가 아닌 reference 형태인 것을 꼭 기억하시기 바랍니다.
class Node<E> {
E data;
Node<E> prev;
Node<E> next;
}아래의 코드는 마찬가지로 원형 이중 연결 리스트의 개념을 바탕으로 각종 기능들을 구현해둔 것입니다. 이번에도 역시 주석을 통해 각각의 메서드가 어떤 역할을 하는지 적어두었습니다. 코드를 천천히 읽으면서 큰 흐름을 파악하시기 바랍니다. 하지만 한 가지만 알려주자면 위에서 이전에 보았던 연결 리스트의 생성자와는 달리 head와 crnt를 NULL로 초기화하지 않고 비어있는 원형 이중 연결 리스트를 생성하고 있습니다. 이는 앞으로의 새로운 노드의 삽입과 삭제 처리가 원활하게 될 수 있도록 도움을 주는 더미 노드입니다.
// 원형 이중 연결 리스트 클래스
public class DbLinkedList<E> {
// 노드 클래스
class Node<E> {
private E data;
private Node<E> prev;
private Node<E> next;
Node() {
data = null;
prev = next = this;
}
Node(E obj, Node<E> prev, Node<E> next) {
data = obj;
this.prev = prev;
this.next = next;
}
}
// 머리(더미) 노드 & 선택 노드
private Node<E> head;
private Node<E> crnt;
// 생성자
public DbLinkedList() {
head = crnt = new Node<>();
}
// 리스트가 비어 있는가를 조사하는 메서드
public boolean isEmpty() {
return head.next == head;
}
// 노드를 검색하는 메서드
public E search(E obj, Comparator<? super E> c) {
Node<E> ptr = head.next;
while (ptr != head) {
if (c.compare(obj, ptr.data) == 0) {
crnt = ptr;
return ptr.data;
}
ptr = ptr.next;
}
return null;
}
// 선택 노드를 출력하는 메서드
public void printCurrentNode() {
if (isEmpty())
System.out.println("선택 노드는 없습니다.");
else
System.out.println(crnt.data);
}
// 모든 노드를 출력하는 메서드
public void dump() {
Node<E> ptr = head.next;
while (ptr != head) {
System.out.println(ptr.data);
ptr = ptr.next;
}
}
// 모든 노두를 거꾸로 출력하는 메서드
public void dumpReverse() {
Node<E> ptr = head.prev;
while (ptr != head) {
System.out.println(ptr.data);
ptr = ptr.prev;
}
}
// 선택 노드를 뒤쪽으로 이동하는 메서드
public boolean next() {
if (!isEmpty() && crnt.next != head) {
crnt = crnt.next;
return true;
}
return false;
}
// 선택 노드를 앞쪽으로 이동하는 메서드
public boolean prev() {
if (!isEmpty() && crnt.prev != head) {
crnt = crnt.prev;
return true;
}
return false;
}
// 노드를 삽입하는 메서드
public void add(E obj) {
Node<E> node = new Node<>(obj, crnt, crnt.next);
crnt.next = crnt.next.prev = node;
crnt = node;
}
// 머리에 노드를 삽입하는 메서드
public void addFirst(E obj) {
crnt = head;
add(obj);
}
// 꼬리에 노드를 삽입하는 메서드
public void addLast(E obj) {
crnt = head.prev;
add(obj);
}
// 선택 노드를 삭제하는 메서드
public void removeCurrentNode() {
if (!isEmpty()) {
crnt.prev.next = crnt.next;
crnt.next.prev = crnt.prev;
crnt = crnt.prev;
if (crnt == head) crnt = head.next;
}
}
// 특정 노드를 삭제하는 메서드
public void remove(Node<E> p) {
Node<E> ptr = head.next;
while (ptr != head) {
if (ptr == p) {
crnt = p;
removeCurrentNode();
break;
}
ptr = ptr.next;
}
}
// 머리 노드를 삭제하는 메서드
public void removeFirst() {
crnt = head.next;
removeCurrentNode();
}
// 꼬리 노드를 삭제하는 메서드
public void removeLast() {
crnt = head.prev;
removeCurrentNode();
}
// 모든 노드를 삭제하는 메서드
public void clear() {
while (isEmpty()) {
removeFirst();
}
}
}👍 글을 마치며
약 3일을 거쳐 리스트 자료구조에 대해서 모두 정리를 하였습니다. 처음에는 양이 얼마 없는 줄 알았으나 적다 보니 중요한 내용들이 많아서 시간이 조금 걸렸습니다. 선형 리스트 같은 경우는 정말 간단하게 리스트를 구현할 수 있지만 연결 리스트 같은 경우는 조금 복잡하다는 것을 공부하면서 많이 느꼈습니다. 그중에서도 커서 연결 리스트는 정말 이해가 되지 않았습니다. 특히 dnext 변수와 두 개의 연결 리스트를 함께 공존해서 움직인다는 것이 신기하기도 했으며 많이 어려웠습니다. 또한 머릿속에 알고 있는 지식을 글로 쉽게 표현하는 것은 매번 힘든 일인 것 같습니다. 하지만 이렇게 블로그를 작성하면서 어휘 능력도 예전보다 늘어나는 것 같고 도움이 많이 되고 있습니다. 앞으로도 새로운 내용에 대해서 여러분들이 쉽게 이해할 수 있도록 좋은 글을 작성하기 위해 노력하겠습니다. 혹시나 오늘 글에서 이해가 되지 않거나 잘못된 내용이 있다는 것을 발견하시면 댓글로 남겨주세요, 빠르게 확인하겠습니다. 감사합니다!
참고 : Do it 자료구조와 함께 배우는 알고리즘 입문 자바 편
'프로그래밍 기초 > Data structure & Algorithm' 카테고리의 다른 글
| 해시에 대해서 (0) | 2021.01.26 |
|---|---|
| 트리에 대해서 (0) | 2021.01.22 |
| 실패율 (0) | 2020.11.21 |
| 비밀지도 (0) | 2020.11.06 |
| 문자열 검색에 대해서 (0) | 2020.10.23 |




