Groo
문자열 검색에 대해서 본문

안녕하세요, 오늘은 여러분들에게 문자열 검색이라는 자료구조에 대해서 설명하려고 합니다.
문자열 검색은 자료구조에서 정말 중요하며 문자열을 자유자재로 다룰 수 있다면 많은 도움이 될 것입니다.
📬 문자열 검색이란?
문자열 검색은 어떤 문자열 안에 특정 문자열이 존재하는지를 조사하고 만약 특정 문자열이 존재한다면 그 문자열의 위치를 찾아내는 자료구조라고 할 수 있습니다. 대표적인 문자열 검색 자료구조로는 브루트 포스법과 KMP법 그리고 Boyer Moore법이 존재합니다.
📸 브루트 포스법
브루트 포스법은 문자열 검색 자료구조 중 가장 간단한 자료구조이며 선형 검색을 확장한 알고리즘으로 단순법, 소박법이라고도 부릅니다. 원본 문자열 텍스트에서 검색하고자 하는 특정 문자열 패턴을 배열을 통해 순차적으로 이동하며 문자열을 찾는 방법입니다.

위의 그림은 원본 문자열 텍스트 "ABABCDEFGHA"에서 특정 문자열 패턴 "ABC"를 검색하는 모습입니다. 원본 문자열 텍스트의 첫 번째 인덱스부터 시작해 3개의 문자가 ABC와 일치하는지 검사하며 앞의 A와 B는 일치하지만 반면에 C는 일치하지 않고 있습니다.
그 후 문자열 패턴의 인덱스를 1칸 뒤로 옮겨 두 번째 인덱스부터 시작해 3개의 문자가 ABC와 일치하는지를 검사하며 만약 일치하지 않다면 이 과정을 문자열 원본 텍스트에서 검색하고자하는 특정 문자열 패턴을 찾을 때까지 계속 반복을 통해 검색합니다.
public class BFmatch {
public static int bfMatch(String text, String pattern) {
int pt = 0;
int pp = 0;
while (pt != text.length() && pp != pattern.length()) {
if (text.charAt(pt) == pattern.charAt(pp)) {
pt++;
pp++;
} else {
pt = pt - pp + 1;
pp = 0;
}
}
if (pp == pattern.length()) {
return pt - pp;
} else {
return -1;
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print("텍스트를 입력하세요 : ");
String text = scanner.next();
System.out.print("찾고자 하는 패턴을 입력하세요 : ");
String pattern = scanner.next();
int idx = bfMatch(text, pattern);
if (idx == -1) {
System.out.println("입력하신 텍스트에 찾고자하는 패턴이 존재하지 않습니다.");
} else {
int length = 0;
for (int i = 0; i < idx; i++) {
length += text.substring(i, i + 1).getBytes().length;
}
length += pattern.length();
System.out.println((idx + 1) + "번째 문자부터 일치합니다.");
System.out.println("텍스트 : " + text);
System.out.printf(String.format("패턴 : %%%ds\n", length), pattern);
}
}
}위의 코드는 브루트 포스법 문자열 검색 자료구조를 코드로 구현해본 것이며 bfMatch 메소드에 원본 문자열 텍스트와 검색하고자 하는 특정 문자열을 넘겨주어 앞에서 설명한 배열 속 구조와 같이 순차적으로 반복하며 특정 문자열이 존재하는지를 판별합니다.
코드 속 가장 중요한 부분은 while 반복문의 조건으로 pt와 pp의 변수 값이 매개변수로 전달받은 각각의 문자열의 길이와 같지 않을 때까지 반복하며 아래의 몇 가지 조건에 맞게 원본 문자열에서 특정 문자열 검색을 성공하였는지 또는 실패하였는지를 알려줍니다.
🎨 String.indexOf 메서드로 문자열 검색
Java 언어의 String 클래스는 문자열을 검색하는 indexOf 메소드와 lastIndexOf 메소드를 제공합니다. 위의 메서드는 모두 매개변수로 전달한 특정 문자열이 포함되어 있는지를 검사하며 만약 특정 문자열이 존재한다면 문자열의 시작 인덱스 값을 제공해줍니다.
indexOf 메소드는 lastIndexOf 메소드와 같은 문자열에 대해 특정 문자열이 여러 개 존재할 시 가장 앞에 위치한 문자열의 시작 인덱스를 반환하지만 lastIndexOf 메소드는 이와 달리 가장 마지막에 위치한 문자열의 시작 인덱스를 제공해주는 차이가 존재합니다.
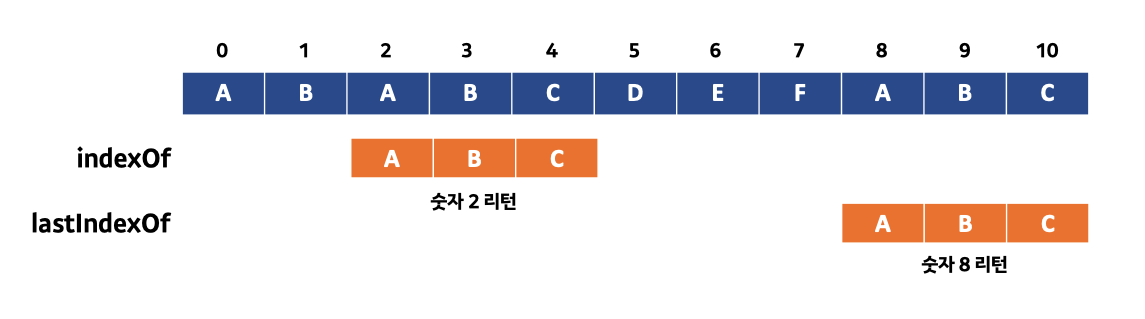
아래의 코드는 indexOf 메소드와 lastIndexOf 메소드를 활용해 문자열 검색 자료구조를 구현한 것이며 정말 간단한 구조여서 따로 설명을 하지 않고도 이해가 될 것입니다. 그러나 한 가지 유의사항이라면 indexOf 메소드와 lastIndexOf 메소드를 호출했을 때 만약 원본 문자열에서 특정 문자열이 존재하지 않을 시 -1이라는 값을 리턴해주면서 특정 문자열이 존재하지 않다는 것을 알려줍니다.
public class IndexOfTester {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print("텍스트를 입력하세요 : ");
String text = scanner.next();
System.out.print("찾고자 하는 패턴을 입력하세요 : ");
String pattern = scanner.next();
int idx1 = text.indexOf(pattern);
int idx2 = text.lastIndexOf(pattern);
if (idx1 == -1) {
System.out.println("입력하신 텍스트에 찾고자하는 패턴이 존재하지 않습니다.");
} else {
int len1 = 0;
for (int i = 0; i < idx1; i++) {
len1 += text.substring(i, i + 1).getBytes().length;
}
len1 += pattern.length();
int len2 = 0;
for (int i = 0; i < idx2; i++) {
len2 += text.substring(i, i + 1).getBytes().length;
}
len2 += pattern.length();
System.out.println("텍스트 : " + text);
System.out.printf(String.format("패턴 : %%%ds\n", len1), pattern);
System.out.println("텍스트 : " + text);
System.out.printf(String.format("패턴 : %%%ds\n", len2), pattern);
}
}
}⛳️ KMP법
KMP법은 다른 문자를 만나면 패턴을 1칸씩 옮긴 다음 다시 패턴의 처음부터 검사하는 브루트 포스법과는 다르게 중간 검사 결과를 효율적으로 사용하는 알고리즘입니다. KMP법을 활용한다면 이전에 검사했던 위치 결과를 버리지 않고 이를 적극 재활용합니다.
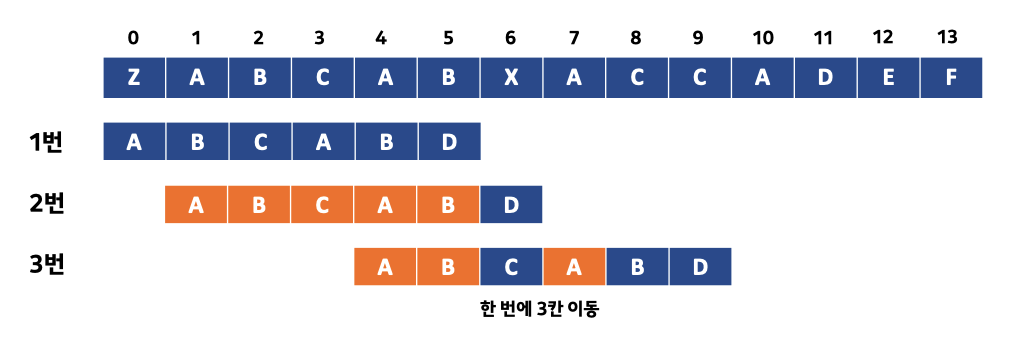
위의 그림을 통해 KMP법을 설명하면 기존의 브루트 포스법과 같은 경우 2번 상황 이후 3번 상황에서 문자열 패턴을 한 칸 뒤로 이동시킨 후 다시 원본 문자열과 검사를 진행할 것이지만 KMP법과 같은 경우는 이미 원본 문자열의 4, 5번째 인덱스의 값과 문자열 패턴의 1, 2번째 인덱스 값이 일치하다는 점을 이용해 이미 검사를 마친 부분은 제외하고 문자열 패턴의 C부터 다시 검사를 진행합니다.
이것이 바로 KMP법의 핵심이라고 할 수 있습니다. 이전에 검사했던 위치 결과를 버리지 않고 텍스트와 패턴의 겹치는 부분을 찾아내어 그 정보들을 다시 재활용해 검사를 다시 시작할 위치를 구합니다. 이런 방법으로 패턴을 최소의 횟수로 옮겨 효율을 높입니다.
public class KMPmatch {
public static int kmpMatch(String text, String pattern) {
int pt = 1;
int pp = 0;
int[] skip = new int[pattern.length() + 1];
skip[pt] = 0;
while (pt != pattern.length()) {
if (pattern.charAt(pt) == pattern.charAt(pp)) {
skip[++pt] = ++pp;
} else if (pp == 0) {
skip[++pp] = pp;
} else {
pp = skip[pp];
}
}
pt = pp = 0;
while (pt != text.length() && pp != pattern.length()) {
if (text.charAt(pt) == pattern.charAt(pp)) {
pt++;
pp++;
} else if (pp == 0) {
pt++;
} else {
pp = skip[pp];
}
}
if (pp == pattern.length()) {
return pt - pp;
} else {
return -1;
}
}
}
위의 코드는 KMP법을 실제 코드로 구현한 것이며 가장 위의 While문의 역할은 몇 번째 문자부터 다시 검색을 시작해야 할지 찾아내는 기능을 수행하며 아래의 While문은 실질적으로 원본 문자열과 패턴을 서로 비교하고 검색하는 과정을 진행하고 있습니다.
그러나 몇 번째 문자부터 다시 검색을 시작해야 할지 계산하는 과정 속에서 KMP법은 높은 효율을 보여주지 못하며 브루트 포스법보다는 복잡하고 뒤에서 배울 Boyer Moore법과는 성능이 같거나 좋지 않아서 실제 프로그램 개발 시 자주 사용되고 있지는 않습니다. 혹시 KMP법에 대해서 조금 더 자세히 알아보며 관련 정보들을 상세히 얻고 싶다면 아래의 블로그 글을 여러분께 적극 추천드립니다.
KMP : 문자열 검색 알고리즘
문자열 검색이 뭐지? 워드프로세서를 사용할 때 찾기 기능을 사용한적 있을 겁니다. 브라우저에서도 Ctrl+F 단축키를 눌러 검색할 수 있습니다. 아래 이미지는 브라우저에서 "테이프"를 검색했
bowbowbow.tistory.com
📊 Boyer Moore법
Boyer Moore법은 브루트 포스법을 개선한 KMP법보다 효율이 더 우수하고 간단하여 실제로 문자열 검색에 가장 널리 사용되는 알고리즘입니다. 이 알고리즘은 독특하게 패턴의 마지막 문자부터 앞쪽으로 검사를 진행하면서 만약 일치하지 않는 문자가 존재한다면 특정 조건에 맞게 문자열 패턴을 이동시키면서 원본 문자열과 패턴을 비교하여 문자열을 검색하는 자료구조라고 할 수 있습니다.
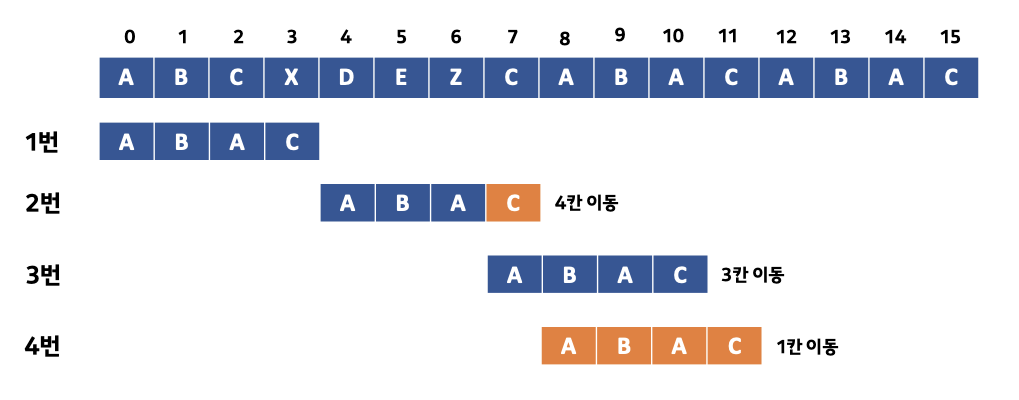
위의 그림을 통해 Boyder Moore법에 대해 설명하면 먼저 1번 상황에서 원본 문자열의 3번째 인덱스 값과 문자열 패턴의 마지막 값을 서로 비교합니다. 그러나 서로의 값이 일치하지 않고 문자열 패턴에는 X 값이 아무것도 존재하지 않는다는 것을 판단하여 문자열 패턴의 크기 n만큼 4칸을 이동한 것을 볼 수 있습니다. 그 후 2번 상황에서는 원본 문자열의 7번째 인덱스 값과 문자열 패턴의 마지막 값이 일치하기에 그다음 원본 문자열의 6번째 인덱스 값과 문자열 패턴의 2번째 인덱스 값을 서로 비교하는 과정을 거칩니다.
그러나 이 둘은 서로의 값이 불일치하여 문자열 패턴의 2번째 인덱스를 기준으로 n만큼 4칸을 이동하여 실질적으로 총 3칸을 이동했습니다. 그 후 원본 문자열의 10번째 인덱스 값과 문자열 패턴의 마지막 값을 비교하는 과정을 거쳤으나 이 과정 속에서 두 값이 서로 일치하지 않아 문자열 패턴 속 A가 존재하는지를 찾기 위해 1칸씩 이동을 하는 과정을 거칩니다. 그러한 과정 속에서 문자열 패턴을 한 칸 이동시켰을 때 원본 문자열과 문자열 패턴이 일치되었으며 최종적으로 원본 문자열에서 문자열 패턴 검색을 성공했습니다.
public class BMmatch {
public static int bmMatch(String text, String pattern) {
int pt;
int pp;
int txtLen = text.length();
int patLen = pattern.length();
int[] skip = new int[Character.MAX_VALUE + 1];
for (pt = 0; pt <= Character.MAX_VALUE; pt++) {
skip[pt] = patLen;
}
for (pt = 0; pt < patLen - 1; pt++) {
skip[pattern.charAt(pt)] = patLen - pt - 1;
}
while (pt < txtLen) {
pp = patLen - 1;
while (text.charAt(pt) == pattern.charAt(pp)) {
if (pp == 0) return pt;
else {
pp--;
pt--;
}
}
pt += (skip[text.charAt(pt)] > patLen - pp) ? skip[text.charAt(pt)] : patLen - pp;
}
return -1;
}
}위의 코드는 앞에서 설명했던 Boyer Moore법을 실제 코드로 구현한 것이며 전체적인 구조는 위에서 설명했던 내용과 동일하게 구현되어 있어 코드를 천천히 읽으면서 따라간다면 어렵지 않고 빠르게 이해할 수 있을 것이라고 생각하여 설명을 생략합니다.
👍 글을 마치며
오늘은 오랜만에 자료구조 및 알고리즘의 기초 개념에 대해서 글을 작성했습니다. 그중 오늘의 주제인 문자열 검색 자료구조는 실제로 알고리즘 등 다양한 문제풀이를 할 때 사용 빈도가 높으며 관련 내용과 개념들을 숙지한다면 훨씬 수월하게 문제를 풀 수 있다고 생각합니다. 대표적으로 문자열 검색이 실생활에서 사용되는 예시는 웹 페이지 상에서 Ctrl F 기능을 사용하면 사용자가 찾고 싶은 단어를 바로 찾을 수 있는 기능이 오늘 배운 문자열 검색 자료구조를 통해 구현되었다는 이야기를 들은 적 있습니다. 이처럼 문자열 검색은 매우 중요하고 자주 사용되니 집중적인 공부가 필요합니다. 이번에 글을 작성하기 위해 저 또한 문자열 검색에 대해서 공부를 했으나 브루트 포스법과 Boyer Moore법에 대해서는 어렵지 않게 이해가 되었으나 KMP법에 대해서는 아직도 헷갈리고 잘 이해가 되지 않아 다른 분들의 글들을 많이 참고하여 공부를 하였습니다. 그렇기에 KMP법에 대해 작성한 글에서는 잘못된 오류가 있을 수도 있기에 양해 부탁드리며 댓글로 문제점과 피드백을 남겨주신다면 이를 잘 숙지하여 글을 수정하고 저 또한 많이 배울 수 있을 것 같습니다.
참고 : Do it 자료구조와 함께 배우는 알고리즘 입문 자바 편




