Groo
재귀에 대해서 본문

안녕하세요, 오늘은 수많은 알고리즘 중 대표적인 알고리즘인 재귀에 대해 알아보려고 합니다.
여러분도 재귀에 대해서는 많이 들어보았을 것입니다, 그러한 만큼 사용 빈도가 다른 알고리즘보다 높고 중요합니다.
🤔 재귀에 대해서 들어보셨나요?
재귀는 어떤 사건이 자기 자신을 포함하고 다시 자기 자신을 사용하여 정의될 때 재귀적이라고 합니다. 아래의 그림을 보시죠 화면 가운데에 다시 화면이 나타납니다. 또한 그 화면 가운데에 똑같은 화면이 반복되어 나타납니다. 이제 재귀의 개념이 이해가 되셨나요?

📈 재귀를 활용한 팩토리얼 구현하기!
이번에는 위에서 배운 재귀의 개념을 활용하여 재귀를 활용한 팩토리얼을 구해보겠습니다. 먼저 팩토리얼이라는 것이 무엇인지에 대해서 설명하겠습니다. 팩토리얼은 아래의 예시와 같이 사용자에게 정수를 입력받아 그 정수로부터 0이 되기 전까지의 곱셉 값입니다.
팩토리얼의 공식 및 방법
1. 0! = 1 (0의 팩토리얼은 1입니다.)
2. n > 0이면 n! = n x (n - 1)! (n이 정수라면 n의 값이 0이 되기 전까지의 모든 값을 곱합니다.)
위의 공식을 사용한다면 어렵지 않게 재귀를 활용하여 팩토리얼을 구할 수 있을 것입니다. 그럼 먼저 프로그램을 구현하기 전 재귀를 활용하여 어떤 구조로 프로그램을 작동시킬 것인지 구상하도록 하겠습니다. 아래의 사진은 직접 손으로 재귀를 구현한 것입니다.

위의 구조는 정말 간단합니다. factorial 함수의 인자로 정수 3을 전달하였으며 인자로 전달된 값이 0보다 클 경우 재귀의 방식대로 factorial함수를 추가로 호출하며 매개변수로는 기존 인자의 값보다 1 작은 값을 전달합니다. 그러나 만약 인자의 값이 0이라면 재귀의 호출을 멈추고 1을 리턴합니다. 그 후 이전에 호출된 함수들의 값을 순차적으로 리턴하고 최종적으로 6이라는 값이 출력됩니다.
public class Factorial {
public static int factorial(int input){
if(input > 0) return input * factorial(input - 1);
else return 1;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print("정수를 입력해주세요 : "); int input = scanner.nextInt();
System.out.println(input + "의 펙토리얼은 " + factorial(input) + "입니다.");
}
}위의 구조와 코드를 함께 본다면 조금 더 쉽게 이해를 할 수 있을 것입니다. 또한 자료구조와 알고리즘을 공부할 때는 빈 공책에 코드의 흐름에 따라 값이 바뀌는 모습을 직접 손으로 그려보며 공부한다면 머리로만 생각하는 것 보다 쉽게 이해하실 수 있을 것입니다.
💁♂️ 직접 재귀와 간접 재귀의 차이점은?
직접 재귀와 간접 재귀의 차이는 직접, 간접 이 두 가지의 단어에 의미가 부여되어있습니다. 저희가 위에서 구현한 팩토리얼 프로그램은 직접 재귀 방법입니다. 그 이유는 무엇일까요? 위를 보시죠, 저희는 factorial 함수를 직접적으로 호출을 하고 있습니다.
직접 재귀와 간접 재귀의 차이점
1. 직접적으로 재귀 함수의 이름으로 호출을 당당하게 진행한다. (직접 재귀 방식)
2. 다른 함수를 통해 간접적으로 재귀 함수의 이름을 호출한다. (간접 재귀 방식)
그럼 간접 재귀는 무엇일까요? 예를 들어보겠습니다. A라는 함수를 저희는 앞으로 계속 재귀 방식을 통해 호출할 것입니다. 그러나 이 A함수를 직접적으로 호출하지 않고 B라는 함수를 통해 A함수를 호출하는 것을 보고 바로 간접 재귀 방식이라고 부릅니다.
🔍 재귀 알고리즘의 분석
이번에는 재귀 알고리즘을 분석하기 위한 하향식과 상향식 분석에 대해서 알아보도록 하겠습니다. 아래 코드 속 recur 메서드는 재귀 호출을 하는 메서드이며 recur 메서드 속 재귀 호출을 2회 실행하고 있습니다. 이러한 것을 순수하게 재귀적이라고 부릅니다.
public class Recur {
public static void recur(int x){
if(x > 0){
recur(x - 1);
System.out.println(x);
recur(x - 2);
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print("정수를 입력해주세요 : "); int input = scanner.nextInt();
recur(input);
}
}위의 재귀 메서드는 꽤 구조가 복잡하여 전략적으로 분석해야 합니다. 여기서는 recur 메서드를 하향식, 상향식 두 방법으로 분석합니다. 먼저 위의 프로그램을 하향식 방법으로 분석 해보겠습니다. 하향식 방법으로 분석을 한다면 아래와 같은 순서로 이루어집니다.
하향식 분석 (매개변수 4 전달)
1. recur(3)을 실행합니다.
2. 4를 출력합니다.
3. recur(2)를 실행합니다.
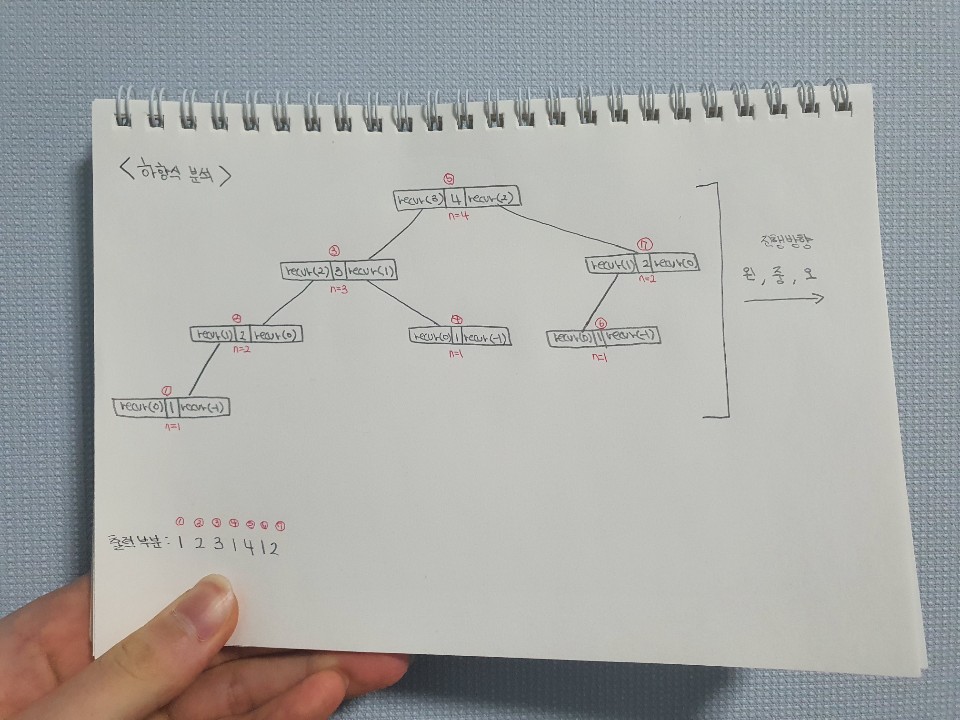
위의 구조는 프로그램을 하향식 분석 방법으로 풀어낸 것입니다. 프로그램의 코드에서도 볼 수 있듯이 매개변수로 인자가 전달된다면 프로그램의 순서는 왼쪽에서 중앙, 중앙에서 오른쪽으로 진행됩니다. 만약 중앙에 위치를 하였다면 인자로 전달된 값을 출력합니다.
그렇다면 상향식 분석은 어떨까요? 하향식 분석과는 반대로 아래쪽부터 쌓아 올리며 분석합니다. recur 메서드는 인자 n이 양수일 때만 실행하므로 인자의 최소 값 1부터 생각을 하면 됩니다. 그 후에도 똑같이 최종 매개변수까지 아래의 숫자들을 검토하면 됩니다.
상향식 분석 (최종 매개변수 4 전달)
1. recur(0)을 실행합니다. (최소 값 1부터 진행)
2. 1을 출력합니다.
3. recur(-1)을 실행합니다.

위의 구조는 상향식 분석 방법으로 풀어낸 것입니다. recur 매서드의 인자로 전달되는 -1과 0은 아무 기능을 하지 않습니다. 0 이상의 정수 인자들만이 recur 메서드에서 재귀를 실행합니다. 이 특징을 살려 코드를 분석한다면 조금 더 쉽게 이해할 수 있을 것입니다.
📚 재귀를 활용한 하노이의 탑 구현하기!
오늘 배운 재귀를 마지막으로 정리하는 의미로 재귀를 활용하여 하노이의 탑을 구현하는 예제를 한 번 구현해보겠습니다. 먼저 하노이의 탑은 작은 원반 위에, 큰 원반이 아래에 위치할 수 있도록 원반을 3개의 기둥 사이에서 옮기는 문제입니다. 한 번 풀어보시죠!
하노이의 탑의 조건
1. 모든 원반은 크기가 다르고 처음에는 모든 원반이 첫 번째 기둥에 위치한다.
2. 원반은 1개씩만 옮길 수 있고 큰 원반을 작은 원반 위에 쌓을 수 없다.
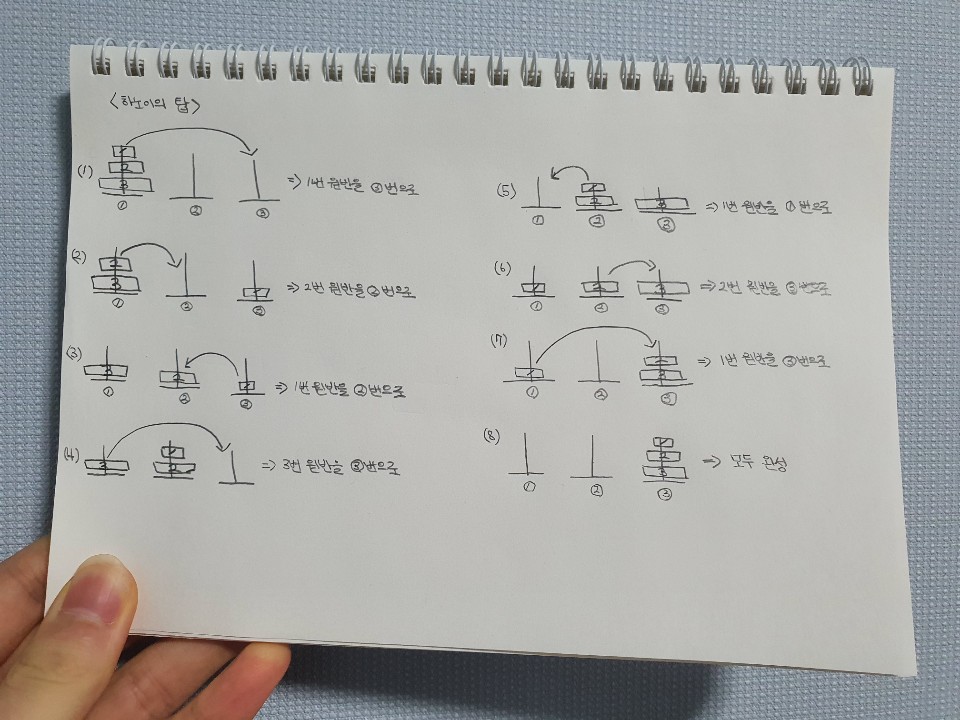
위의 구조는 원반 3개를 옮길 때 가장 최소한으로 옮길 수 있는 방법을 나타내 보았습니다. 그러나 이 구조도 역시 공식이 존재합니다. 원반의 개수가 3개가 아닌 4개, 5개 등 이어도 같은 구조의 방식으로 하노이의 탑의 문제를 풀어낼 수 있습니다. 특징을 찾아봅시다.

위의 구조를 보면 3개의 원반에서 가장 큰 원반인 숫자 3 원반을 먼저 3번째 기둥에 이동시키고 있습니다. 그 작업을 수행하기 위해 숫자 3 원반 위에 위치한 숫자 1, 2 원반을 그룹 단위로 본 후 2번째 기둥에 옮긴다면 숫자 3 원반을 쉽게 이동시킬 수 있을 것입니다.
그 후 그룹 단위로 묶어둔 숫자 1, 2 원반을 다시 3번째 기둥의 속한 숫자 3 원반 위에 올려준다면 정상적으로 하노이의 탑 문제를 수행할 수 있습니다. 즉 원반의 개수와 상관없이 하노이의 탑 문제를 쉽게 구할 수 있다는 것을 알게 된 것이죠!
public class Hanoi {
// input개의 원반을 x 번에서 y 번으로 이동시킵니다.
public static void move(int input, int x, int y){
if(input > 1) move(input - 1, x, 6 - x - y);
System.out.println("원반[" + input + "]를 " +
x + "기둥에서 " + y + "기둥으로 옮겼습니다.");
if(input > 1) move(input - 1, 6 - x - y, y);
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("하노이의 탑");
System.out.print("원반 개수를 입력해주세요 : "); int input = scanner.nextInt();
move(input, 1, 3); // 1번 기둥의 input개의 원반을 3번 기둥으로 옮김니다.
}
}위의 프로그램은 기둥 번호를 정수 1, 2, 3으로 나타내며 기둥 번호의 합이 6이므로 시작 기둥, 목표 기둥이 어느 기둥이더라도 중간 기둥은 6-x-y로 구할 수 있습니다. 원반은 input개이므로 move매서드는 조건에 따라 재귀적으로 메서드를 호출하고 있습니다.
👍 글을 마치며
오늘은 알고리즘의 대표적인 유형 중 하나인 재귀 알고리즘에 대해서 알아보았습니다. 재귀 알고리즘은 다른 알고리즘들보다 과정과 내용이 복잡해 어떤 방법으로 설명을 하면 좋을지에 대해서 많이 구상하였습니다. 그러던 중 저는 제가 직접 풀이한 문제와 구조도를 정리하여 그것을 사진으로 찍어 업로드한다면 더욱 이해하기 쉬울 것이라고 생각을 하였으며 여러분들에게도 추천해주는 방법이기도 하였습니다. 재귀 알고리즘뿐만이 아닌 다른 알고리즘 등 복잡한 일을 할 때는 그것을 그림으로 나타내면 쉽게 해결할 수 있습니다.
참고 : Do it 자료구조와 함께 배우는 알고리즘 입문 자바 편
'프로그래밍 기초 > Data structure & Algorithm' 카테고리의 다른 글
| 크레인 인형뽑기 게임 (2) | 2020.07.15 |
|---|---|
| 정렬에 대해서 (0) | 2020.04.02 |
| 큐에 대해서 (2) | 2020.02.13 |
| 스택에 대해서 (0) | 2020.02.12 |
| 이진 검색과 시간 복잡도에 대해서 (0) | 2020.02.12 |




